Click here to find me on the arXiv.

Click here to find me on MathSciNet (subscription required.)

• 

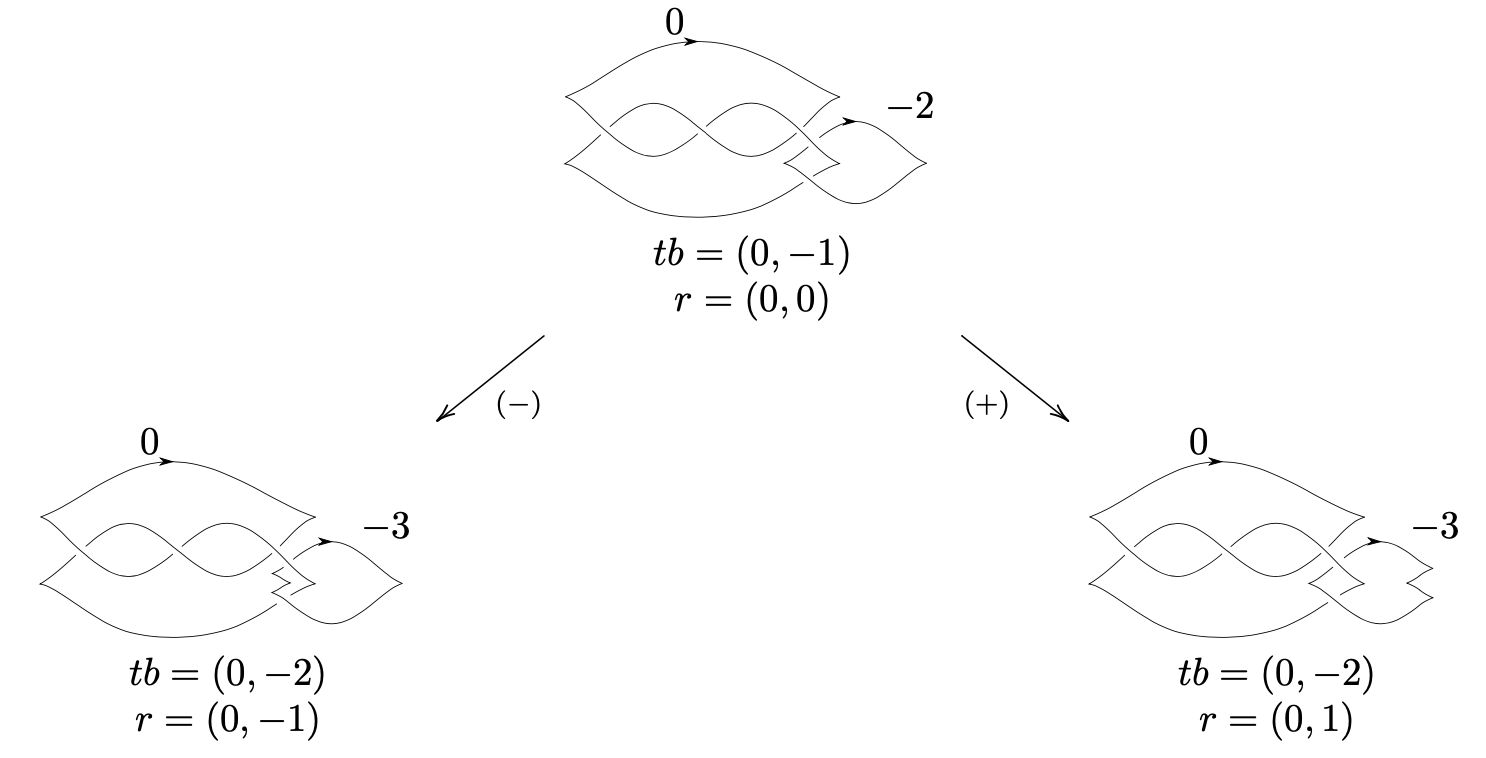
  Framed instanton homology of surgeries on L-space knots

  Tye Lidman, Juanita Pinzon-Caicedo, Christopher Scaduto

  Submitted

  An important class of three-manifolds are L-spaces, which are rational homology spheres with the smallest possible Floer homology. For knots with an instanton L-space surgery, we compute the framed instanton Floer homology of all integral surgeries. As a consequence, if a knot has a Heegaard Floer and instanton Floer L-space surgery, then the theories agree for all integral surgeries. In order to prove the main result, we prove that the Baldwin-Sivek contact invariant in framed instanton Floer homology is homogeneous with respect to the absolute ℤ/2-grading, but not the ℤ/4-grading.

• 

  The Topological Slice Genus of Satellite Knots

  Peter Feller, Allison N. Miller, Juanita Pinzon-Caicedo

  Submitted

  This paper presents evidence supporting the conjecture that in the topological category the slice genus of a satellite knot P(K) is bounded above by the sum of the slice genera of K and P(U). Our main result establishes this conjecture for a variant of the topological slice genus, the Z-slice genus. Notably, the conjectured upper bound does not involve the algebraic winding number of the pattern P. This stands in stark contrast with the smooth category, where for example there are many genus 1 knots whose (n, 1)- cables have arbitrarily large smooth 4-genera. As an application, we show that the (n, 1)-cable of any knot of 3-genus one (e.g. the figure-eight or trefoil knot) has topological slice genus at most 1, regardless of the value of n ∈ N. Further, we show that the lower bounds on the slice genus coming from the Tristram-Levine and Casson-Gordon signatures cannot be used to disprove the conjecture.

• 

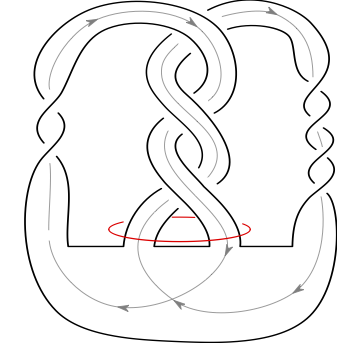
  Satellites of Infinite Rank in the Smooth Concordance Group

  Matthew Hedden, Juanita Pinzon-Caicedo

  Submitted

  We conjecture that satellite operations are either constant or have infinite rank in the concordance group. We reduce this to the difficult case of winding number zero satellites, and use $SO(3)$ gauge theory to provide a general criterion sufficient for the image of a satellite operation to generate an infinite rank subgroup of the smooth concordance group $\mathcal{C}$. Our criterion applies widely, notably to scores of unknotted patterns for which the corresponding operators on the topological concordance group are zero. We raise some questions and conjectures regarding satellite operators and their interaction with concordance.

• 

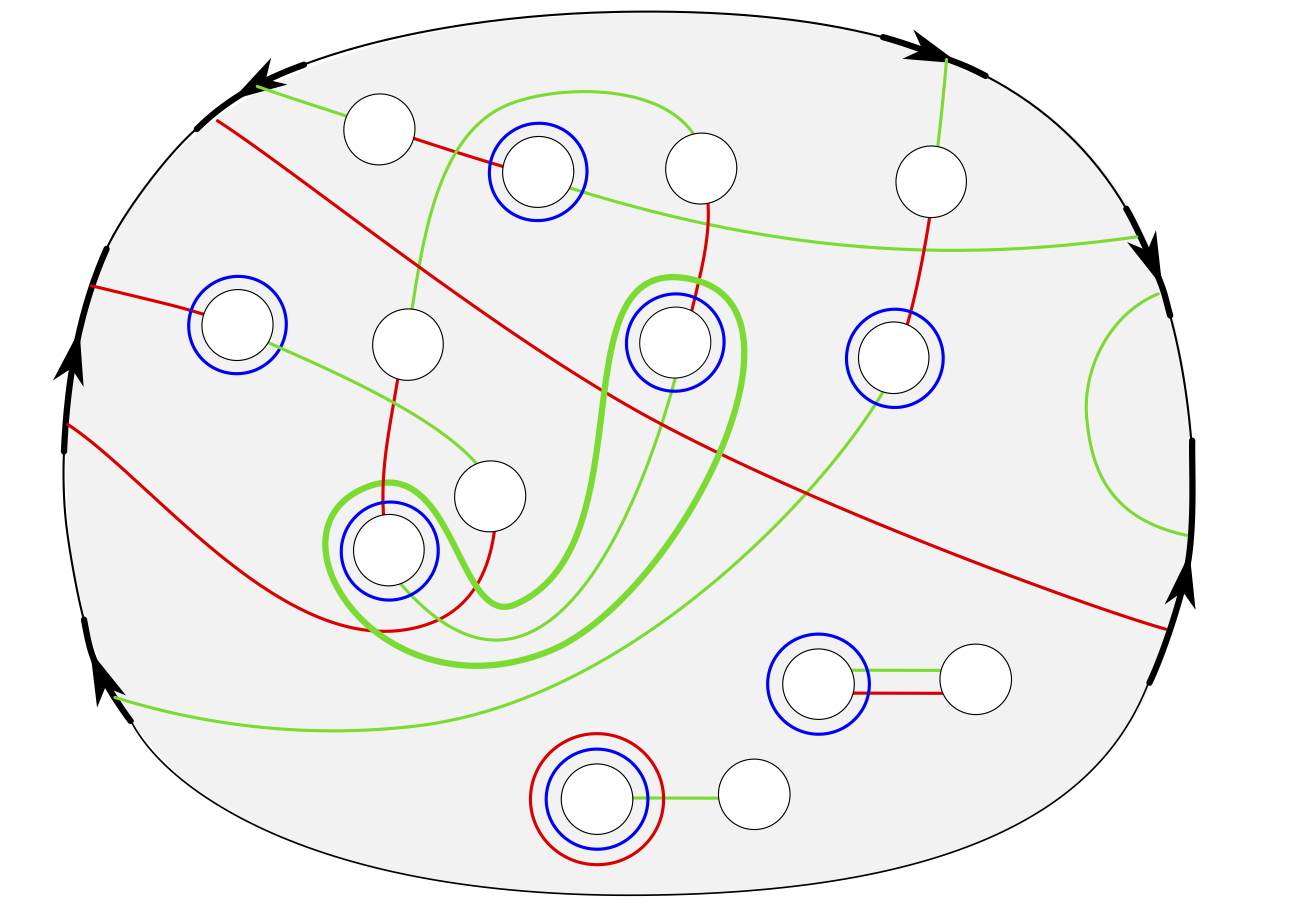
  Trisections of 4-manifolds with Boundary

  Nickolas A. Castro, David T. Gay, Juanita Pinzon-Caicedo

  Proc. Natl. Acad. Sci. USA 115 (2018), no. 43, 10861–10868.

  Given a handle decomposition of a 4-manifold with boundary, and an open book decomposition of the boundary, we show how to produce a trisection diagram of a trisection of the 4-manifold inducing the given open book. We do this by making the original proof of the existence of relative trisections more explicit, in terms of handles. Furthermore, we extend this existence result to the case of 4-manifolds with multiple boundary components, and show how trisected 4-manifolds with multiple boundary components glue together.

• 

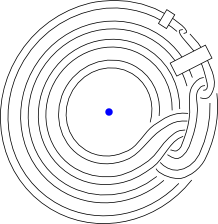
  Independence of Iterated Whitehead Doubles

  Juanita Pinzon-Caicedo

  Proc. Amer. Math. Soc. 147 (2019), no. 3, 1313–1324.

  A theorem of Furuta and Fintushel-Stern provides a criterion for a collection of Seifert fibred homology spheres to be independent in the homology cobordism group of oriented homology 3-spheres. In this article we use these results and some 4-dimensional constructions to produce infinite families of positive torus knots whose iterated Whitehead doubles are independent in the smooth concordance group.

• 

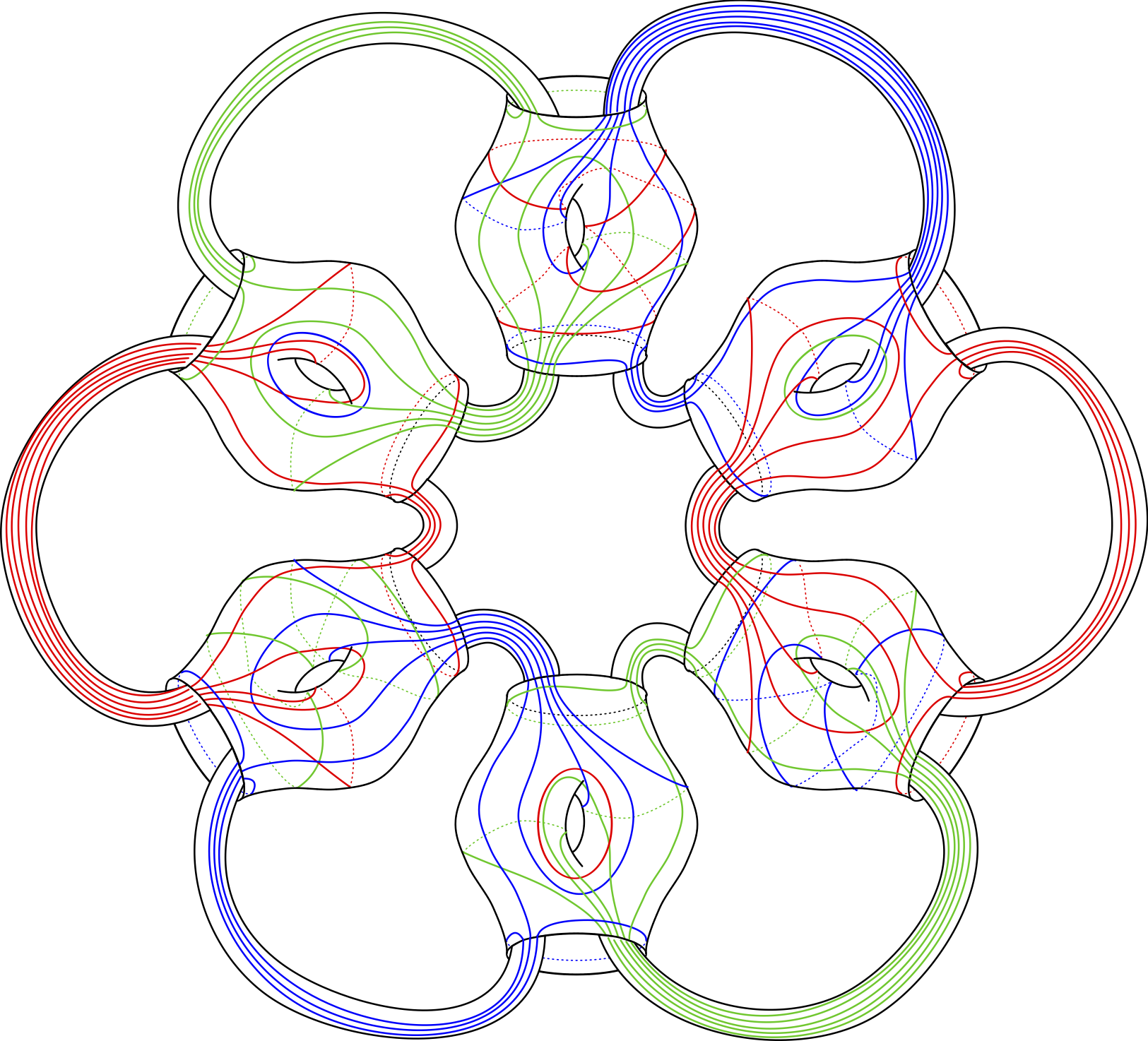
  Diagrams for Relative Trisections

  Nickolas A. Castro, David T. Gay, Juanita Pinzon-Caicedo

  Pacific J. Math. 294 (2018), no. 2, 275–305.

  We establish a correspondence between trisections of smooth, compact, oriented 4--manifolds with connected boundary and diagrams describing these trisected 4--manifolds. Such a diagram comes in the form of a compact, oriented surface with boundary together with three tuples of simple closed curves, with possibly fewer curves than the genus of the surface, satisfying a pairwise standardness condition. This should be thought of as the 4--dimensional analog of a sutured Heegaard diagram for a sutured 3--manifold. We also give many foundational examples.

• 

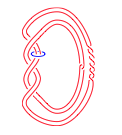
  Independence of Satellites of Torus Knots in the Smooth Concordance Group

  Juanita Pinzon-Caicedo

  Geom. Topol. 21 (2017), no. 6, 3191–3211.

  The main goal of this article is to obtain a condition under which an infinite collection ℱ of satellite knots (with companion a positive torus knot and pattern similar to the Whitehead link) freely generates a subgroup of infinite rank in the smooth concordance group. This goal is attained by examining both the instanton moduli space over a 4-manifold with tubular ends and the corresponding Chern-Simons invariant of the adequate 3-dimensional portion of the 4-manifold. More specifically, the result is derived from Furuta's criterion for the independence of Seifert fibred homology spheres in the homology cobordism group of oriented homology 3-spheres. Indeed, we first associate to ℱ the corresponding collection of 2-fold covers of the 3-sphere branched over the elements of ℱ and then introduce definite cobordisms from the aforementioned covers of the satellites to a number of Seifert fibered homology spheres. This allows us to apply Furuta's criterion and thus obtain a condition that guarantees the independence of the family ℱ in the smooth concordance group.

• 

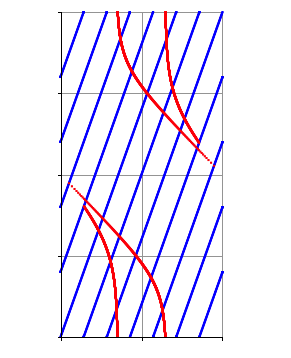
  Traceless SU(2) representations of 2-stranded tangles

  Yoshihiro Fukumoto, Paul Kirk, Juanita Pinzon-Caicedo

  Math. Proc. Cambridge Philos. Soc. 162 (2017), no. 1, 101–129.

  Given a 2-stranded tangle T contained in a ℤ-homology ball Y, we investigate the character variety R(Y,T) of conjugacy classes of traceless SU(2) representations of π1(Y \ T). In particular we completely determine the subspace of binary dihedral representations, and identify all of R(Y, T) for many tangles naturally associated to knots in S 3. Moreover, we determine the image of the restriction map from R(T, Y) to the traceless SU(2) character variety of the 4-punctured 2-sphere (the pillowcase). We give examples to show this image can be non-linear in general, and show it is linear for tangles associated to pretzel knots.

• 

  Gauge Theory and Knot Concordance

  Latinx in Math, Duke Topology Seminar, MSU Topology Seminar

  Knot concordance can be regarded as the study of knots as boundaries of surfaces embedded in spaces of dimension 4. Specifically, two knots K0 and K1 are said to be smoothly concordant if there is a smooth embedding of the 2—dimensional annulus S1 × [0, 1] into the 4—dimensional cylinder S3 × [0, 1] that restricts to the given knots at each end. Smooth concordance is an equivalence relation, and the set of smooth concordance classes of knots, C, is an abelian group with connected sum as the binary operation. The algebraic structure of C, the concordance class of the unknot, and the set of knots that are topologically slice but not smoothly slice are much studied objects in low-dimensional topology. Gauge theoretical results on the nonexistence of certain definite smooth 4-manifolds can be used to better understand these objects. In particular, the study of anti-self dual connections on 4-manifolds can be used to shown that (1) the group of topologically slice knots up to smooth concordance contains a subgroup isomorphic to Z^\infty, and (2) satellite operations that are similar to cables are not homomorphisms on C.

  Poster
• 

  La dimensión 4 y la concordancia de nudos

  XXI Congreso Colombiano de Matematicas

  La meta principal de la topología geométrica es la clasificación de las variedades según su estructura (topológica, suave, simpléctica, etc.). En dimensión 4 la historia es especial: es la única dimensión en la que una variedad puede admitir un número infinito de estructuras suaves no equivalentes y la única dimensión en la que existen variedades homeomorfas pero no difeomorfas a R^4. A su vez, la concordancia de nudos es el estudio de los nudos como fronteras de superficies encajadas en espacios de dimensión 4. La diferencia entre estructuras topológicas y estructuras suaves en dimensión 4 está estrechamente relacionada con la concordancia de nudos. En la charla explicaré una faceta de ésta relación.

• 

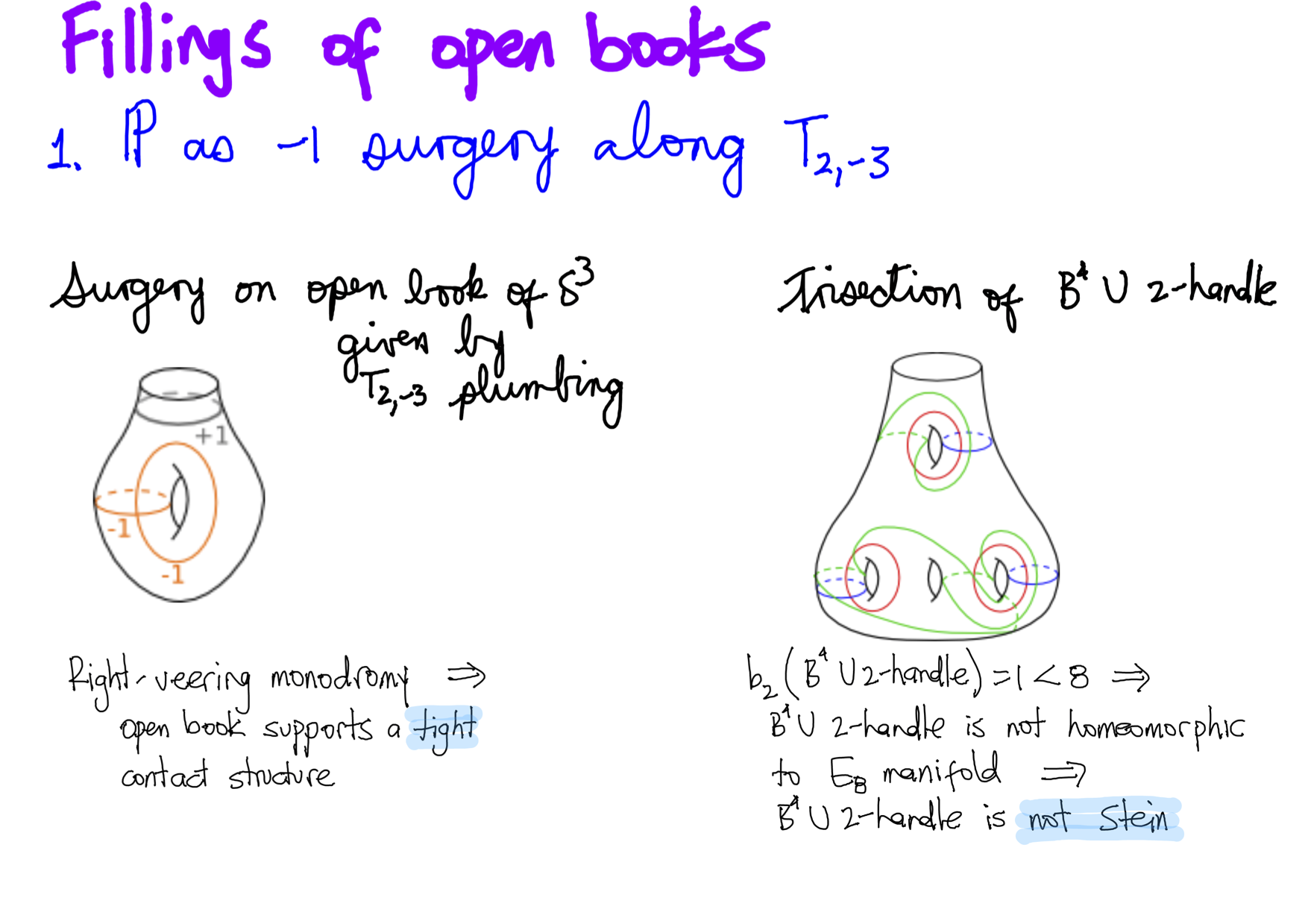
  Examples of relative trisections

  AMS Sectional NCSU, Georgia Tech, AMS Sectional St. Thomas University, HIM

  Trisections of 4-manifolds relative to their boundary were introduced by Gay and Kirby in 2012. They are decompositions of 4-manifolds that induce open book decomposition in the bounding 3-manifolds. This talk will focus on diagrams of relative trisections and will be divided in two. In the first half I will focus on trisections as fillings of open book decompositions and I will present different fillings of different open book decompositions of the Poincare homology sphere. In the second half I will show examples of trisections of pieces of some of the surgery techniques that result in exotic 4-manifolds.

  Slides1 Slides2
• 

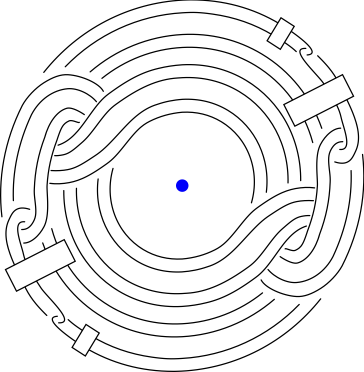
  Iterated Whitehead Doubles are Independent

  MPIM

  In the 1980’s Furuta and Fintushel-Stern applied the theory of instantons and Chern-Simons invariants to develop a criterion for a collection of Seifert fibred homology spheres to be independent in the homology cobordism group of oriented homology 3-spheres. These results, together with some 4-dimensional constructions can be used to show that iterated Whitehead doubles of positive torus knots are independent in the smooth concordance group.

• 

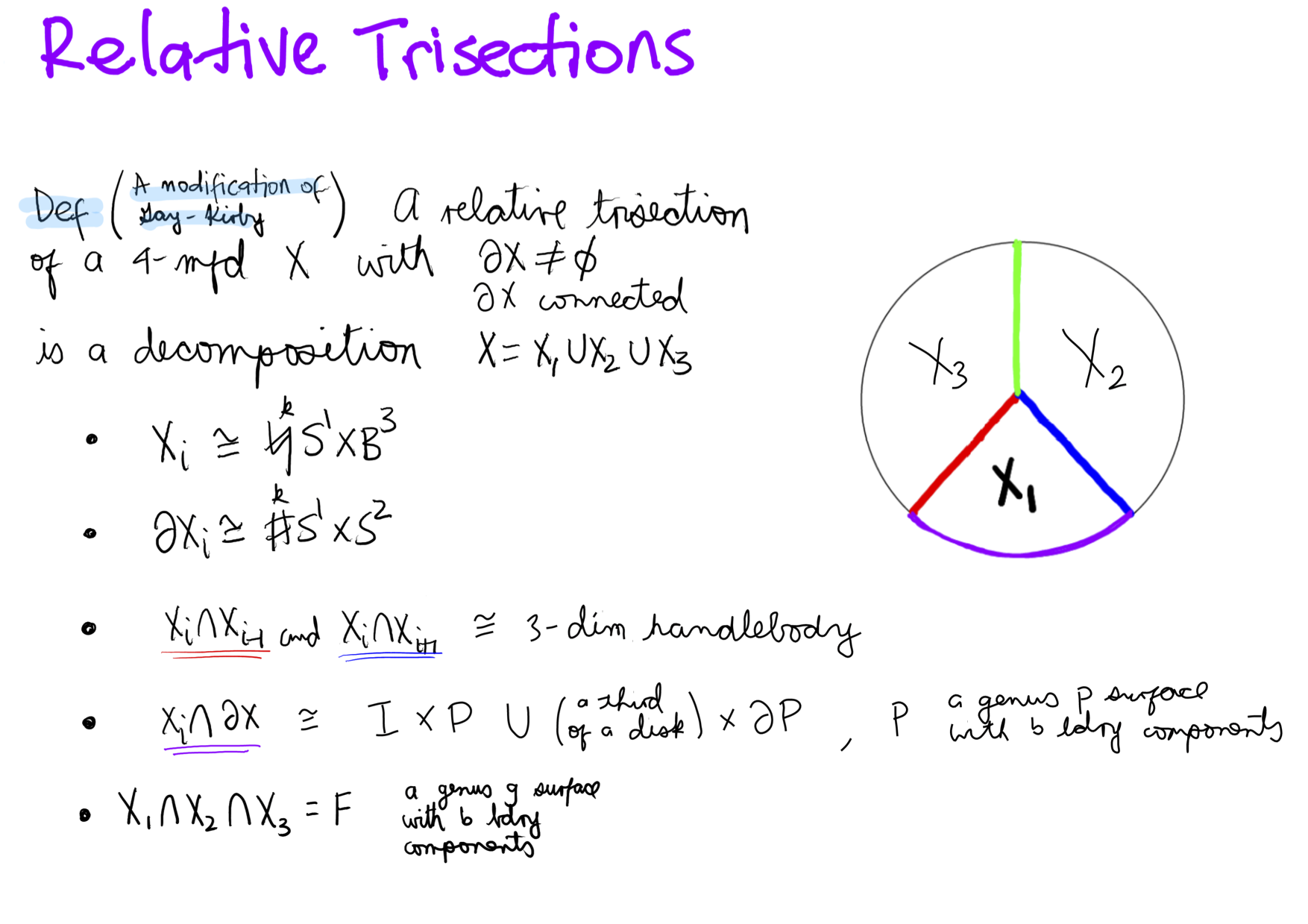
  An Overview of Relative Trisections

  University of Iowa, AMS Sectional UGA, BIRS, SUNY Buffalo

  Based on the notion of trisections of closed 4--manifolds of Gay and Kirby, Nick Castro and myself developed a rigorous definition of relative trisections as a generalization of trisections to 4--manifolds with boundary. In the talk I will present the basics of relative trisections starting with their relationship to open book decompositions of the bounding manifolds. I will then introduce a stabilization operation that gives rise to a statement about the uniqueness of relative trisections, thus complementing Gay and Kirby's proof of the existence of relative trisections. Finally, I will introduce the notion of diagrams of relative trisections and describe a method to recover the open book decomposition of the bounding manifold from the trisection diagrams. 

  Slides Video
• 

  Construcciones de 3-variedades y la esfera de Poincaré

  Matemáticas por estudiantes, Universidad de Los Andes

  En 1910 Henri Poincare publicó un articulo en el que afirmaba que los grupos de homología eran suficientes para determinar si una 3-variedad es la 3-esfera S3. Cuatro años más adelante Poincaré mismo publicó la descripción de una 3-variedad con los mismos grupos de homología que S3 pero distinta a esta última. Hoy en día este espacio se conoce como la esfera de Poincaré y parte de su encanto radica en que se puede describir de distintas maneras, todas construcciones de enorme importancia en el estudio de 3-variedades. La idea de la charla es describir algunas de estas construcciones a través de la esfera de Poincaré. Algunas de las construcciones que intentaré describir son cirugía de Dehn, espacios recubridores ramificados y espacios cocientes.

• 

  Independence of Whitehead Doubles of Torus Knots in the Smooth Concordance Group

  Georgia Tech, Brandeis University, Knots in the Triangle, University of Georgia, IAS, University of Minnesota

  In the 1980’s Furuta and Fintushel-Stern applied the theory of instantons and Chern-Simons invariants to develop a criterion for a collection of special homology spheres to be independent in the homology cobordism group of oriented homology 3-spheres. Hedden and Kirk then use the aforementioned criterion to establish conditions under which an infinite family of Whitehead doubles of positive torus knots are independent in the smooth concordance group. In the talk, I will review some of the definitions and constructions involved in the proof by Hedden and Kirk and I will introduce some topological constructions that simplify and extend their argument. 

  Slides
• 

  3-Esferas de Homología

  Oaxaca

  Una 3-esfera de homología es una variedad diferencial cerrada y orientada que tiene mismos grupos de homología de la 3-esfera. En el mini-curso presentaré diferentes construcciones de este tipo de objetos, introduciré los invariantes de Rokhlin y Casson para finalmente hablar de la estructura algebraica del grupo de cobordismo de 3-esferas de homología.

• 

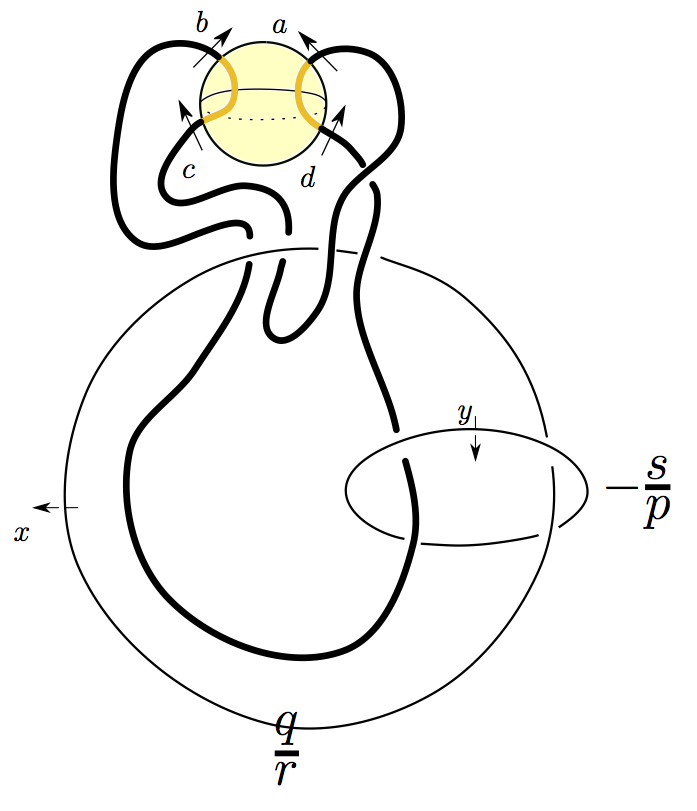
  Traceless SU(2) representations of 2-stranded tangles

  Michigan State, Louisiana State University

  Given a codimension 2 submanifold A⊂X define R(X,A) as the space of traceless SU(2) representations of π_1(X\A) modulo conjugation. For Y a 3-manifold and K⊂Y a knot, Kronheimer-Mrowka defined the Instanton Knot Homology of (Y,K) as the homology of a chain complex whose groups are generated by the elements of R(Y,K). In the talk we describe a method to determine R(S^3,K) whenever K is a torus or pretzel knot.

  Slides